Pengertian dan Rumus Bangun Datar
Pada kesempatan kali ini kita akan membahas materi mengenai bangun datar mulai dari pengertian, macam-macam bangun datar dan juga rumus bangun datar. Untuk itu simak penjelasan dibawah ini.
Pengertian Bangun Datar
Bangun datar adalah sebuah bidang dengan tampilan dua dimensi yang dibatasi oleh garis lurus ataupun garis lengkung.
Macam-macam Bangun Datar dan Rumusnya
Ada berbagai macam jenis bangun datar yang umum dalam pelajaran matematika, seperti persegi, persegi panjang, segi tiga, trapesium, jajargenjang, belah ketupat, layang-layang, dan lingkaran,
Persegi
Persegi adalah sebuah bangun datar yang terdiri dari 4 sisi, keempat sisinya memiliki panjang yang sama dan membentuk sudut siku-siku.
Rumus Persegi
Luas persegi
L = s x s = s2
Keliling persegi
K = 4 x s
Diagonal persegi
d = √s² + s²
Keterangan :
s = panjang sisi persegi
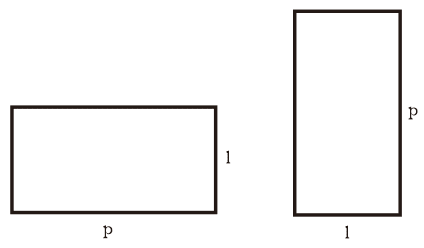
Persegi Panjang
Persegi panjang adalah bangun datar yang bentuknya berupa segiempat memiliki 2 pasang sisi yang sejajar dan sama panjang serta keempat sudutnya membentuk sudut siku-siku.
Rumus Persegi Panjang
Luas persegi panjang
L = p x l
Keliling persegi panjang
K = 2p + 2l = 2 x (p + l)
Diagonal persegi panjang
d = √p² + l²
Keterangan :
p = panjang persegi panjang, dan l = lebar persegi panjang
Segitiga
Segitiga adalah bangun datar yang dibatasi 3 buah sisi dan memiliki 3 buah titik sudut.
Jika dilihat berdasarkan panjang sisinya, segitiga dapat dibedakan menjadi 3, yakni segitiga sama sisi, segitiga sama kaki, dan segitiga sembarang. Sedangkan jika dilihat dari besar sudutnya maka segitiga dapat dibedakan menjadi 3, yakni segitiga lancip, segitiga tumpul, dan segitiga siku-siku.
Rumus Segitiga
Luas segitiga
L = ½ x a x t
Keliling segitiga
K = a + b + c
Tinggi segitiga
t = (2 × Luas) ÷ a
Alas segitiga
a = (2 × Luas) ÷ t
Panjang sisi miring segitiga siku-siku bisa dicari dengan menggunakan rumus Phytagoras (A2 + B2 = C2)
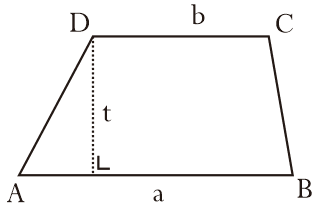
Trapesium
Trapesium adalah bangun datar yang bentuknya berupa segiempat dengan sepasang sisi yang sejajar.
Rumus Trapesium
Luas trapesium
L = ½ x (a1 + a2) x t
Keliling trapesium
Tinggi trapesium
Keterangan :
a1 dan a2 = sisi-sisi sejajar pada trapesium, dan t = tinggi trapesium
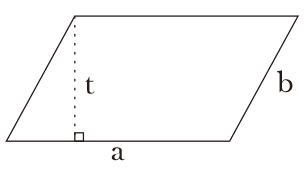
Jajar Genjang
Jajar genjang adalah sebuah bangun datar yang bentuknya berupa segiempat dengan sisi-sisi yang berhadapan sama panjang dan sejajar, serta sudut-sudut yang berhadapan sama besar.
Rumus Jajar Genjang
Luas jajar genjang
L = a x t
Keliling jajar genjang
K = 2 × (a + b)
Sisi alas jajar genjang
a = (K ÷ 2) - b
Sisi miring jajar genjang
a = (K ÷ 2) - af
Keterangan :
a = panjang alas jajargenjang, t = tinggi jajargenjang, dan b = sisi-sisi miring
Layang-layang
Layang-layang adalah sebuah bangun datar dengan bentuk berupa segiempat dan memiliki 2 pasang sisi yang berdekatan sama panjang dan kedua diagonalnya berpotongan tegak lurus.
Rumus Layang-layang
Luas
L = ½ × d1 × d2
Keliling
K = a + b + c + d atau K = 2 × (a + c)
Diagonal 1
d1 = 2 × L ÷ d2
Diagonal 2
d2 = 2 × L ÷ d1
Sisi miring
a atau b a = (½ × K) - c
c atau d c = (½ × K) - a
Belah Ketupat
Belah ketupat adalah bangun datar yang bentuknya berupa segiempat, keempat sisinya memiliki panjang yang sama dan kedua diagonalnya berpotongan tegak lurus.
Rumus Belah Ketupat
Luas belah ketupat
L = ½ × d1 × d2
Keliling belah ketupat
K = s + s + s + s atau K = s × 4
Sisi-sis belah ketupat
s = K ÷ 4
Diagonal 1
d1 = 2 × L ÷ d2
Diagonal 2
d2 = 2 × L ÷ d1
Lingkaran
Lingkaran adalah sebuah bangun datar yang terbentuk dari himpunan semua titik yang memiliki jarak yang sama dari satu titik ke titik lainnya.
Rumus Lingkaran
Diameter lingkaran
d = 2 × r
Jari-jari lingkaran
r = d ÷ 2
Luas lingkaran
Keliling lingkaran
Menjari jari-jari lingkaran
Mencari jari-jari jika luas lingkaran diketahui
Sekian artikel mengenai pengertian dan rumus bangun datar, terima kasih semoga bermanfaat.
Referensi:
Artikel berjudul "8 Rumus Bangun Datar, Pengertian, Jenis, dan Contohnya" diakses 09 Januari 2021, dari https://www.advernesia.com/blog/matematika/bangun-datar/


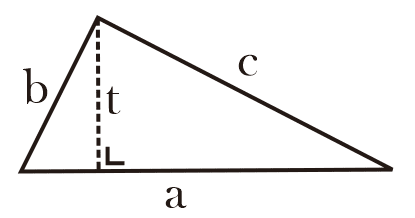








Posting Komentar untuk "Pengertian dan Rumus Bangun Datar"
Ingatlah untuk selalu menjaga komentar tetap sopan dan mengikuti pedoman komunitas kami